SUGGESTIONS ABOUT THE CONSTRUCTION OF THE GIZA TEMPLES
© Colin Reader
[extracted from an email dated 28 Sep 2000]
As far as the material for the ramps is concerned, I don't actually feel that stone rubble would offer much of an advantage over sand in terms of strength, but both would be far better than mudbrick. The reason I think this is that the limestone at Giza consists of a matrix of old sand grains, shell and coral fragments, cemented to form a rock. Under pressure or when loaded, the weak limestones can disaggregate - break down into these component pieces. Sand grains on the other hand are (generally) single quartz grains - each of which has a large compressive strength. The other thing about windblown sand, which abounds at Giza, is that the sand is 'well sorted' - that is it will have fairly uniform grain size and will be fairly well rounded. In a pile, individual grains will fit quite well together - imagine a cube constructed from polystyrene balls - you see them occasionally!! The more the surface contact between grains - the more any load will be distributed. Putting all that together, with sand you get a load distributed well across strong quartz grains - little potential for failure of the embankment (but see below - stability); put the same load on more angular limestone rubble, the load gets concentrated at the points of contact which, as the rubble will be of different sizes and shapes, will be smaller - leading to intense localised stress concentration in the weaker limestone and localised failure! This failure wouldn't be enough to destabilise most embankments though. The big disadvantage of sand is that it will flow so that any embankment will have side slopes equal to the angle of repose (about 28 degrees to the horizontal for loose sand). A high embankment would have a huge area at the base. On balance, therefore, I think rubble ramps are better for high structures.
I think that pyramid construction and temple construction need a fundamentally different approach. A temple will be, at the most, 9 or 10m high, whereas a pyramid will be 10's or even over a hundred metres high. From the outset, therefore, your approach has to be different - you know you're going to have to lift masonry to the top of a pyramid, and whatever construction method you adopt needs to facilitate that from the outset. Not only that but by the time they came to build at Giza, they'd learned lessons from Meidum and Dashur about structural stability problems - possibly resulting from the use of not very well squared masonry in the pyramid core. In the Great Pyramid, at least, the core masonry is fairly well squared - a finish achieved by repeatedly offering up the individual blocks, trimming them and checking the fit. So for a pyramid you need, not only to be able to get your blocks to the top, but once they get there they need multiple handling. Smaller blocks (if 2.5 tonnes can be considered small) are best suited for that.
If you only need to lift masonry for temples a few meters up, then you can get away with larger blocks and most of the cyclopean masonry at Giza is not particularly well squared - so didn't need multiple handling. So that brings me back to the use of sand infill. In the sketches I e-mailed on Sunday, I considered that they would have effectively buried the temple in sand as it grew. But as you've pointed out it would take a lot of sand and effort. So I've done some calculations to investigate the stability of a cyclopean temple in which sand is only placed on the inside. The first calculation of the attachment (below) details what I've done - you perhaps don't need to study it - it's just the support to what I've summarised here.
That the stability assessment shows is that if you have 8m of sand on one side of a cyclopean wall, it will not collapse - the sheer weight of the masonry prevents this. What's really surprising is that, from a temporary works point of view, a less substantial wall would take a lot more effort to build because, if you use the sand-fill method you'd need sand outside the wall as well as inside to support the growing structure! Another benefit of this is that you don't need all four walls in place to be able to start to bury the structure in sand - a free standing wall would appear to be OK.
I discussed above the relative strength of sand and limestone rubble (granite rubble would, of course be by far the best - but there would have been comparatively little of that). While there's little chance of the sand fill actually failing - it won't crush - an embankment used as a ramp to lift blocks of stone (such as shown on my sketches) may be structurally unstable and the embankment might collapse. To investigate this I've done a slope stability assessment of a typical 8m high, 10m wide (at the top) embankment used perhaps to construct the temples at Giza (see attachment below). If this had side-slopes at the angle of repose for loose sand the embankment would only be some 40 m wide at the widest point and, with a gradient of 1 in 10, 80m long - not too big. I modelled the load imposed by a large (200 tonne) block of stone and, as I suspected, such an embankment would be relatively stable - with the only instability apparently the sloughing of sand at the crest of the embankment. Even here, though, the factors of safety (min 1.7) are OK and are even better for a short-lived earthwork (many old railway embankments have FoS = 1.2 - there's a cutting in Bradford with FoS = 1 and it's moving!).
What this shows - and it's an initial rough assessment, but OK for present purposes - is that for temple construction a sand ramp leading to a completely sand filled structure would provide a feasible method of constructing the temples at Giza. You would also need a small man-ramp for the lads on the ropes on the opposite face of the temple to the ramp used for hauling masonry.
I agree that the Sphinx temple itself is not the greatest exponent of the art as the blocks are smaller, the source of the stone (the Sphinx enclosure) is near and the west wall is actually a rock cutting. Would this suggest less practised (and therefore earlier) builders??? Of course I'd like to think so!
In summary then, these initial calculations suggest to me that if you are building a relatively low structure, the use of cyclopean masonry and sand ramps and infill is entirely feasible and not beyond the realms of possibility. What the Egyptians had an abundance of was labour and sand - and using this technique they would need to fill only the inside of the structure and build a masonry ramp on one side and a man-ramp on the opposite side (OK still a lot of effort - but more than the hard labour involved in breaking the masonry down into 2.5 tonne blocks with hammer stones?). Neither ramp would need to have any role in supporting the walls.
If you made the walls thinner - i.e. with smaller masonry - you would in fact need more sand as you would have to fill outside as well as inside; much more effort and much more sand at an angle of repose of 28 degrees!
As long as the blocks didn't get too close to the edge of the ramps, the sand would be an entirely suitable material to take the weight of even the biggest blocks. Sand, however, needs gently sloping sides so the higher you go with your ramp the bigger it will become.
Calculation of stability of wall for a cyclopean structure filled with sand as a temporary construction activity
1 Theory
Soil Mechanics theory for the calculation of lateral earth pressure (that is the overturning thrust that will act on a wall which is retaining a body of soil) is governed by two primary assumptions:
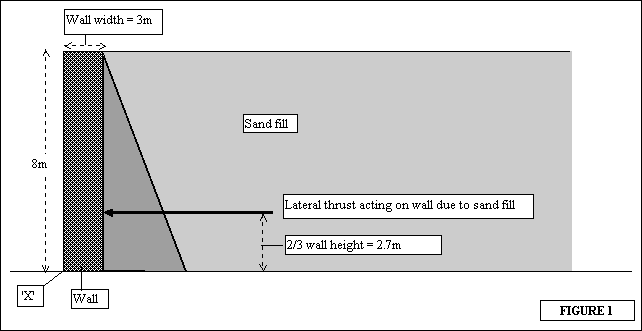
- the pressure is proportional to the height of the wall and so adopts a triangular distribution (see figure 1 below)
- the lateral thrust that this pressure develops results in a force acting at 1/3 of the wall height.
2 Calculations
The lateral earth pressure (p) = Kgh where
K = coefficient of lateral earth pressure (0.3 for a loose sand fill against a masonry wall)
g = weight per cubic metre = 1.8 tonnes/cubic metre
h = wall height = 8m in this case
p at the base of the wall = 0.3 x 1.8 x 8 = 4.3 tonnes/m2
The overturning thrust that this represents P = 1/2ph = 0.5 x 4.3 x 8 = 17.2 tonnes/linear m (i.e. the triangular area on the figure).
This force acts horizontally at a height of 2.7m above the ground, resulting in a destabilising moment of 17.2 x 2.7m = 46.5 tonnes.
The stability of the wall itself, results from its mass. At 8m high and 3m wide, the wall has a cross sectional area of 24m2 per linear metre.
Masonry will be particularly heavy; data used by Dieter Arnold (Building in Egypt) suggests a figure of 2.7 tonnes/m3 assuming a 200 tonne block with dimensions 8 x 3 x 3m (as used in Menkaures' Mortuary Temple).
The mass of this wall, will therefore be 24 x 2.7 = 64.8 tonnes/lin m.
This mass acts vertically downward through the central vertical axis of the masonry, some 1.5m from the outside toe of the masonry (point 'X' on figure 1 below). The restoring moment resulting from the wall's mass is, therefore, 64.8 x 1.5 = 97.2 tonnes.
3 Conclusions
These calculations suggest a restoring moment of 97 t and a disturbing moment, due to the contained sand fill, of 46.5 t. The factor of safety against the collapse of the wall is, therefore, 97.2/ 46.5 = 2.1. A factor of safety of 1 indicates marginal stability, below 1 and the wall would collapse.
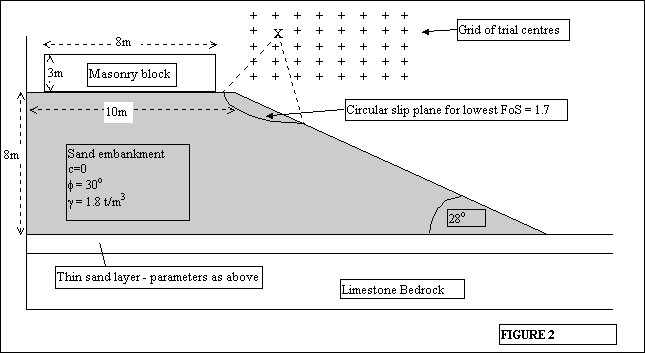
Stability of an 8m high sand embankment with a 200 tonne block resting at the top
1 Method
Using proprietary slope stability software, the stability of a ramp, built manually from sand and used to raise substantial blocks of stone, has been investigated. Loose well graded sand, typical of that sorted by the action of wind and, therefore, found at Giza, can be assumed to have a mass of 1.8 tonnes/m3, however, given the granular nature of sand it will compact to some degree under it's own weight. The sand at the base of the embankment is likely to have a greater density than the 1.8te/m3 used here.
The two other soil-strength parameters needed for the calculation are cohesion [c] which for sand is zero, and the shear strength parameter, phi, which has been assumed to be 30o.
In embankments built from uniform soils such as this, failure typically occurs as a rotational slip along a circular section through the embankment (see figure 2 below).
2 The Model
The model used is shown in figure 2 and represents an 8m high 10m wide embankment with side slopes of 28o. This value (28o) represents the angle of repose of loose, well graded sand - i.e. of sand at Giza.
The embankment rests on a 1m layer of loose sand, overlying limestone bedrock.
To model the load imposed by a limestone masonry block being dragged along, the load imposed by such a block has been calculated and is represented by a uniformly distributed load of 8.5 t/m2. This has been arrived at by dividing the weight of the block (200 t) by the area resting on the ramp (8m x 3m - see Arnold). 200/(8 x 3) = 200/24 = 8.3 t/m2. This load is modelled across 8m of the embankment, however, it is likely that an 8m x 3m x 3m block would be dragged up with the shorter face leading - i.e. the load would be acting across 3m of the embankment cross section. The model is, therefore, conservative.
3 Results of Stability Analysis
Stability is assessed by taking a grid of slip circle centres adjacent to the embankment and, for various radii, comparing the restorative and destabilising forces acting on the embankment. The lowest factor of safety predicted by the analysis was 1.7 for a circle with radius 7m. Other factors of safety derived were in the order of 4 or 5 with some points having greater than 10.
What is noteworthy is that the lowest factor was for a shallow slip as shown on figure 2. This suggests that whilst the body of the embankment will be stable under loading from even the largest blocks of masonry, some slight spalling may occur on the shoulders of the embankment.